Assignment 2

Goals:

The goal of this assignment is to become familiar with a variety of statistical methods and programs. 

Part 1:

For part one of this assignment, I will be analyzing a sample of the test scores from two different high schools in the Eau Claire School District: Eau Claire North and Eau Claire Memorial. These test scores come from standardized tests taken by juniors at both schools.  Throughout the years, Eau Claire Memorial has continued to have the student with the highest test score. This leads the public to question how well the students at Eau Claire North are being taught since there is never a student with the highest test score. I will be analyzing both sets of test scores by looking at the Range, Mean, Median, Mode, Kurtosis, Skewness, and Standard Deviation. Then I will look at the results and determine if the public should actually be concerned with the teaching methods at Eau Claire North. First, I will define each of these terms and then provide the calculation. 

Range: The range is the difference between the highest number and the lowest number. For example, if the highest value in a set of data is 66 and the lowest value is 45, then the range would be 21. In relation to the data sets for this assignment, the range for Eau Claire North is 83 and the Range for Eau Claire Memorial is 91.

Mean: When finding the mean, one is finding the average of a set of values. To find the mean, you add of the values together and then divide by the number of values. The mean for Eau Claire North is 160.92 and Eau Claire Memorial's mean is 158.54.

Median: The median is finding the middle value of a set of values, but the values need to be ranked in order. If the amount of values is an odd number, the value in the middle would be the median. If the amount of values happen to equal an even number, then the difference between the two most middle values would equal the median. The median for Eau Claire North is 164.5, Eau Claire Memorial is 159.5.

Mode: The mode is number that occurs most in a set of observations. Eau Claire North's mode is 170 and Eau Claire Memorial's is 120. 

Kurtosis: This refers to the distribution of a data set. Kurtosis is when the distribution is more peaked or flat compared to the normal distribution. Peaked distribution means a positive kurtosis and a flatter distribution means a negative kurtosis. If the kurtosis is above a +1 or a -1 then it is a significant distribution. The kurtosis for Eau Claire North ended up being -0. 56 Eau Claire Memorial's kurtosis is -1.17.

Skewness: This shows how far away the distribution is from the mean. The distribution can be positively or negatively skewed. The skewness of Eau Claire North is -0.58 and Eau Claire Memorial's is -0.18.

Standard Deviation (SD): This is useful in showing how close the observations are to the mean of the data. So 68% of the data will fall between one standard deviation, 95% will fall between two standard deviations, and 99% will fall between three standard deviations of the mean. To better understand how standard deviation is calculated, I have physically written out the calculations for and Eau Claire Memorial (Figure 1) and Eau Claire North (Figure 2), which you can see below. The standard deviation for Eau Claire Memorial is 27.16 and Eau Claire North's is 23.63.

Figure 1: SD of Eau Claire Memorial's Test Scores

Figure 2: SD of Eau Claire North's Test Scores

Results: 
Although Eau Claire Memorial has continuously had a student achieve the highest score between both schools (198 out of 200), we can tell from the statistics that this doesn't mean that the teaching methods at Memorial are any better. The Mean for Memorial is 158.54 and for North it is 160.92, this shows that the average at North is actually higher than Memorial. The standard deviation also helps to show why North shouldn't be concerned with their test scores. First of all, the SD for North is 23.63 and the SD for Memorial is 27.16. This means that the test scores at North are bunched closer around the mean than Memorial's are. The Memorial test scores are more wide spread which means the scores vary a lot more, which isn't usually a good thing when it comes to test scores. Secondly, knowing that the maximum score a student can get is 200, we can see that most of the scores for North fall above a score of 160.9 which is good because that means over half of the students achieved a score of 80% or higher. Like I said before, the test scores for Memorial are more widespread and have a larger range. I think the mean and standard deviation are both useful statistics when comparing test scores. The mean shows the average of the scores, and the standard deviation displays how close the data clusters around the mean. So to tie everything together, Eau Claire North should not be concerned about their teaching methods because although they didn't have a student with the highest score, their overall test scores were actually higher than Eau Claire Memorial. When looking at test scores, it is more effective to look at all of the scores as a whole, not just an individual score.

Part 2:
For part two of this assignment, I have calculated the Geographic Mean Center of Population at the county level for Wisconsin as well as the Weighted Mean Center of Population for 2000 and 2015. I have also created a map to show my calculations (Figure 3). I will also explain the relationships of the weighted mean centers on the map. But first of all, I will define what these calculations actually mean.

Geographic Mean Center of Population: This is the average of x and y values on a map. So for this assignment, I calculated the geographic mean center of population for the counties in Wisconsin. This is represented by the purple circle on the map in Figure 3. 

Weighted Mean Center of Population: This is similar to the geographic mean center but the weighted mean center includes the frequencies of grouped data. Different points will be weighted more than others. Some counties in Wisconsin have higher populations than others so that would influence the mean center, which is why it would weighted. For this assignment, I compared the weighted mean center for the 2000 population and the 2015 population. The 2000 population mean center is labeled as a red circle and the 2015 population mean center is labeled as a yellow circle on the map in Figure 3.

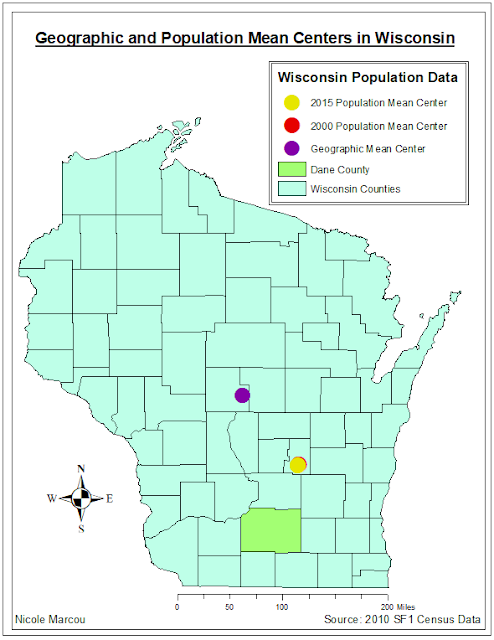Figure 3: Map of Geographic Mean Centers of Population in Wisconsin

Explanation:
By looking at the map, we can see that the 2015 population mean center (yellow) barely moved at all from the 2000 population mean center (red). However, the 2015 population mean center did shift slightly southwest. Each counties population either increased or decreased from the year 2000 to 2015. However, the biggest population increase was located in Dane County, which is labeled in green on the map. In 2000, Dane County's population was 426,526, and in 2015 it jumped to 510,198. That is an increase of over 80,000 people, which makes sense to why the 2015 mean center slightly shifted towards Dane County. A reason to why the population of Dane County increased the most is because that is where the capitol of Wisconsin is located.

Sources:
Census of Agriculture: 2010 SF1 Census Data